動機
就是一維的推廣
Problem
Given a 2D matrix matrix, handle multiple queries of the following type:
- Calculate the sum of the elements of
matrixinside the rectangle defined by its upper left corner(row1, col1)and lower right corner(row2, col2).
Implement the NumMatrix class:
NumMatrix(int[][] matrix)Initializes the object with the integer matrixmatrix.int sumRegion(int row1, int col1, int row2, int col2)Returns the sum of the elements ofmatrixinside the rectangle defined by its upper left corner(row1, col1)and lower right corner(row2, col2).
Example 1:
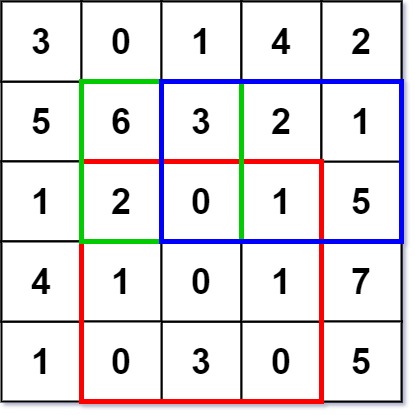
Input[NumMatrix, sumRegion, sumRegion, sumRegion][[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]Output[null, 8, 11, 12]ExplanationNumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200-105 <= matrix[i][j] <= 1050 <= row1 <= row2 < m0 <= col1 <= col2 < n- At most
104calls will be made tosumRegion.
Ver1: WA
假設 1 2 3 4 5 如果要求2 3 4可以用
1 2 3 4去減1,所以取的起點是原本的起點再往後推一格後再扣
不過如果原本的起點是0,像求1 2 3這樣就尷尬了
class NumMatrix:
def __init__(self, ms: List[List[int]]):
self.origing_ms = ms
for i in range(0,len(ms)):
acc = 0
for j in range(0,len(ms[i])):
acc += ms[i][j]
ms[i][j] = acc #(acc,ms[i][j])
#for j in range(0,len(ms[0])):
# acc = 0
# for i in range(0,len(ms)):
# acc += ms[i][j][1]
# ms[i][j] = (ms[i][j][0],acc)
self.ms = ms
def sumRegion(self, r1: int, c1: int, r2: int, c2: int) -> int:
if r1 == r2 and c1 == c2:
return self.origing_ms[r1][c1]
else:
ret = 0
for i in range(r1,r2+1):
ret += self.ms[i][c2] - self.ms[i][c1-1]
return ret
Ver2: AC
解法是替所有非法index回傳0,這樣不論怎麼加或減都沒事
class NumMatrix:
def __init__(self, ms: List[List[int]]):
#self.origing_ms = [[x for x in l] for l in ms]
for i in range(0,len(ms)):
acc = 0
for j in range(0,len(ms[i])):
acc += ms[i][j]
ms[i][j] = acc #(acc,ms[i][j])
#for j in range(0,len(ms[0])):
# acc = 0
# for i in range(0,len(ms)):
# acc += ms[i][j][1]
# ms[i][j] = (ms[i][j][0],acc)
self.ms = ms
self.w = len(ms[0]) if len(ms) > 0 else -1
self.h = len(ms)
def getMS(self,i,j):
if i < 0 or j < 0 or i >= self.h or j >= self.w:
return 0
else:
return self.ms[i][j]
def sumRegion(self, r1: int, c1: int, r2: int, c2: int) -> int:
#if r1 == r2 and c1 == c2:
# return self.origing_ms[r1][c1]
#else:
ret = 0
for i in range(r1,r2+1):
#print(i,c1,c2,self.getMS(i,c2),self.getMS(i,c1-1))
ret += self.getMS(i,c2) - self.getMS(i,c1-1)
return ret