動機
十分有趣
Problem
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the root of a binary tree, return the maximum path sum of any path.
Example 1:
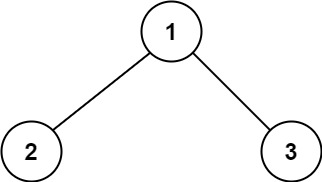
Input: root = [1,2,3]Output: 6Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Example 2:
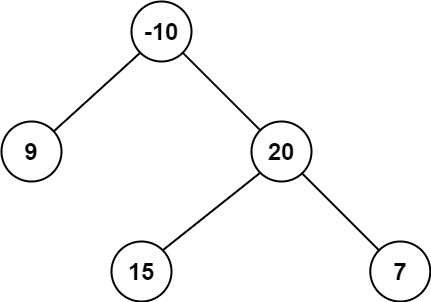
Input: root = [-10,9,20,null,null,15,7]Output: 42Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Constraints:
- The number of nodes in the tree is in the range
[1, 3 * 104]. -1000 <= Node.val <= 1000
Sol
總和有
- 只有左邊
- 只有右邊
- 只有根結點
- 左邊+根結點
- 右邊+根結點
- 左邊+右邊+根結點
如果父節點也想加上去只有3~5的可以把父節點的值也加上去 所以分成兩個回傳值
def dfs(root):
if not root:
return [float('-inf'), float('-inf')]
else:
gLeft, lLeft = dfs(root.left)
gRight, lRight = dfs(root.right)
now_connectable = max(root.val, root.val+lLeft, root.val+lRight)
now_global = max(root.val+lLeft+lRight, gLeft, gRight, now_connectable)
return [now_global, now_connectable]
class Solution:
def maxPathSum(self, root: TreeNode) -> int:
return dfs(root)[0]