動機
複習dfs
Problem
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
class Node { public int val; public List neighbors;}
Test case format:
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
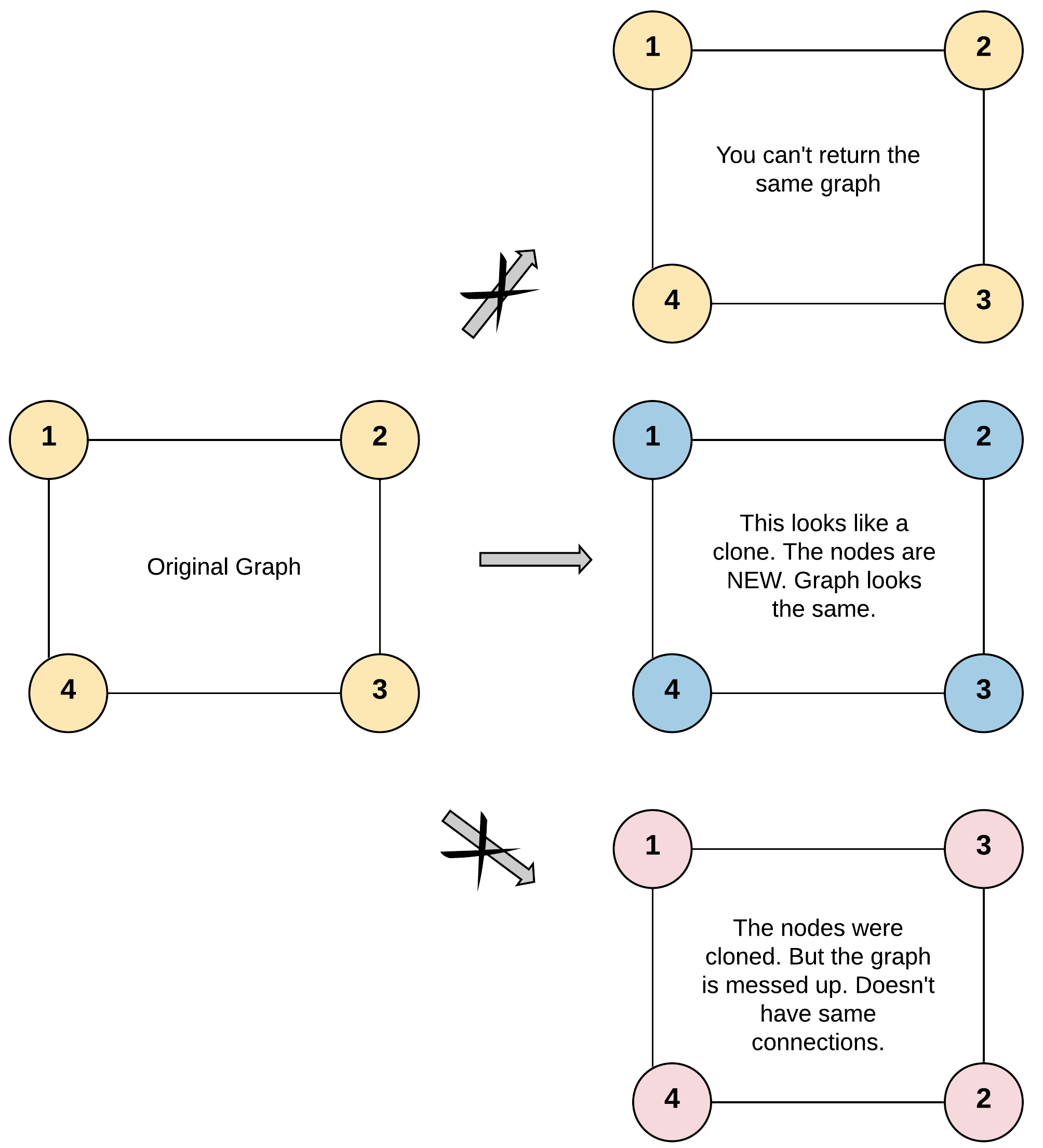
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]Output: [[2,4],[1,3],[2,4],[1,3]]Explanation: There are 4 nodes in the graph.1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
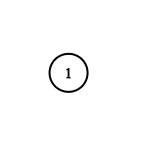
Input: adjList = [[]]Output: [[]]Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = []Output: []Explanation: This an empty graph, it does not have any nodes.
Example 4:
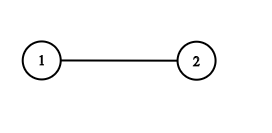
Input: adjList = [[2],[1]]Output: [[2],[1]]
Constraints:
- The number of nodes in the graph is in the range
[0, 100]. 1 <= Node.val <= 100Node.valis unique for each node.- There are no repeated edges and no self-loops in the graph.
- The Graph is connected and all nodes can be visited starting from the given node.
Sol
要記得把生過的node拿出來用
class Solution:
def __init__(self):
self.mem = {}
def cloneGraph(self, node: 'Node') -> 'Node':
if not node:
return None
else:
ret = Node(node.val)
self.mem[node] = ret
for n in node.neighbors:
if n not in self.mem:
ret.neighbors.append(self.cloneGraph(n))
else:
ret.neighbors.append(self.mem[n])
return ret