動機
很有趣的問題,原來python有可以直接算combination的函數…
Problem
Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.
For example, given nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array [2,3,1] also yields the same BST but [3,2,1] yields a different BST.
Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.
Since the answer may be very large, return it modulo 10^9 + 7.
Example 1:
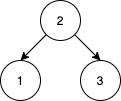
Input: nums = [2,1,3]Output: 1Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.
Example 2:
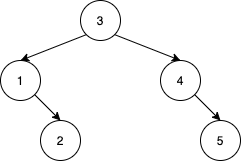
Input: nums = [3,4,5,1,2]Output: 5Explanation: The following 5 arrays will yield the same BST: [3,1,2,4,5][3,1,4,2,5][3,1,4,5,2][3,4,1,2,5][3,4,1,5,2]
Example 3:
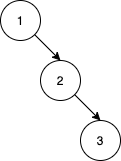
Input: nums = [1,2,3]Output: 0Explanation: There are no other orderings of nums that will yield the same BST.
Example 4:
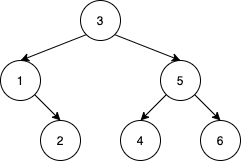
Input: nums = [3,1,2,5,4,6]Output: 19
Example 5:
Input: nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18]Output: 216212978Explanation: The number of ways to reorder nums to get the same BST is 3216212999. Taking this number modulo 10^9 + 7 gives 216212978.
Constraints:
1 <= nums.length <= 10001 <= nums[i] <= nums.length- All integers in
numsare distinct.
Sol
這是BST,所以第一個是root,而比root小的就是在左,其他在右
所以第一個位置不能動,其他的只要個子樹的相對位置不變就好,所以就是在去掉root的剩下格子中,有多少種安排左(右)子樹的方式再乘上左右子樹的組合數
class Solution:
def numOfWays(self, nums: List[int]) -> int:
def f(nums):
if len(nums) <= 1:
return 1
else:
r = [n for n in nums[1:] if n > nums[0]]
l = [n for n in nums[1:] if n < nums[0]]
return comb(len(r)+len(l), len(r))*f(l)*f(r)
return (f(nums)-1) % (10**9 + 7)