動機
複習backtrack
Problem
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:
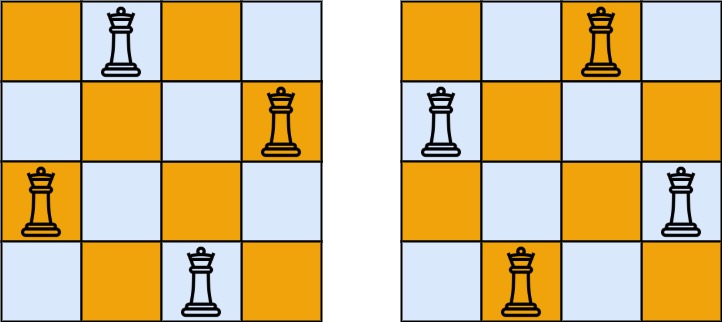
Input: n = 4Output: [[.Q..,...Q,Q...,..Q.],[..Q.,Q...,...Q,.Q..]]Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1Output: [[Q]]
Constraints:
1 <= n <= 9
Sol
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
tbl = []
for _ in range(n):
tmp = []
for _ in range(n):
tmp.append(".")
tbl.append(tmp)
def good(taken, j):
return not any([abs(taken[dep] - j) in [0, len(taken)-dep] for dep in range(len(taken))])
ret = []
def bt(i,taken=[]):
if i == n:
ret.append([''.join(l) for l in tbl])
else:
for x in range(n):
tbl[i][x] = "Q"
if good(taken, x):
bt(i+1, taken+[x])
tbl[i][x] = "."
bt(0)
return ret