動機
你大神還是你大神,滿滿的創意
在BST上做bsearch(太神啦) 帶入範圍
Problem
Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
Example 1:
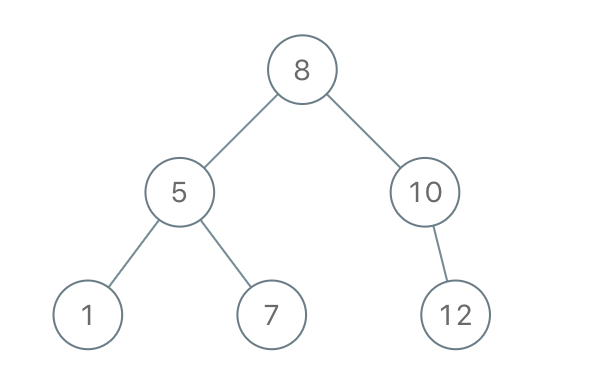
Input: preorder = [8,5,1,7,10,12]Output: [8,5,10,1,7,Leetcode,12]
Example 2:
Input: preorder = [1,3]Output: [1,null,3]
Constraints:
- t
1 <= preorder.length <= 100t1 <= preorder[i] <= 108t- All the values of
preorderare unique.
Sol
在preorder做bsearch,太神啦 範圍要sort? 不用不用 只要符合binary search就好!!
class Solution:
def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:
def dfs(ns):
if not ns:
return None
else:
i = bisect.bisect(ns,ns[0])
ret = TreeNode(ns[0])
ret.left = dfs(ns[1:i])
ret.right = dfs(ns[i:])
return ret
return dfs(preorder)
帶入範圍
class Solution:
def bstFromPreorder(self, ns: List[int]) -> Optional[TreeNode]:
i = 0
def dfs(limit=float('inf')):
nonlocal i
if i >= len(ns) or ns[i] > limit:
return None
else:
ret = TreeNode(ns[i])
i += 1
ret.left = dfs(ret.val)
ret.right = dfs(limit)
return ret
return dfs()