動機
把不要的扣掉!!
Problem
Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 109 + 7.
Note that you need to maximize the answer before taking the mod and not after taking it.
Example 1:
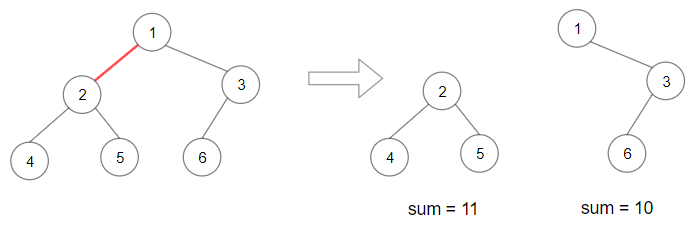
Input: root = [1,2,3,4,5,6]Output: 110Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
Example 2:
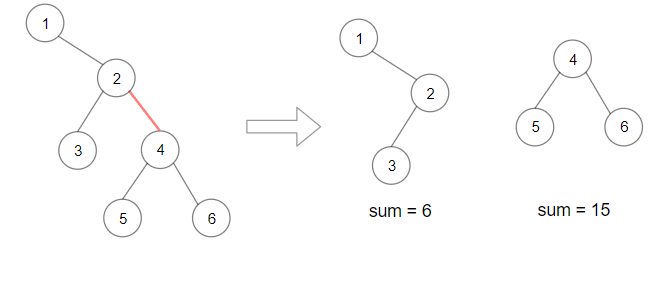
Input: root = [1,Leetcode,2,3,4,null,null,5,6]Output: 90Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Example 3:
Input: root = [2,3,9,10,7,8,6,5,4,11,1]Output: 1025
Example 4:
Input: root = [1,1]Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 5 * 104]. 1 <= Node.val <= 104
Sol
class Solution:
def maxProduct(self, root: Optional[TreeNode]) -> int:
ans = 0
def dfs(r,cb):
if not r:
return 0
else:
left = dfs(r.left,cb)
right = dfs(r.right,cb)
cb(left,right)
return r.val+left+right
total = dfs(root, lambda a,b: None)
def cb(a,b):
nonlocal ans
ans = max(ans, (total-a)*a, (total-b)*b)
dfs(root,cb)
return ans % (10**9 + 7)