動機
1331變成2維
Problem
Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].
The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:
- t
- The rank is an integer starting from
1. t - If two elements
pandqare in the same row or column, then:t- tt
- If
p < qthenrank(p) < rank(q)tt - If
p == qthenrank(p) == rank(q)tt - If
p > qthenrank(p) > rank(q)t
t - If
- The rank should be as small as possible.
It is guaranteed that answer is unique under the given rules.
Example 1:
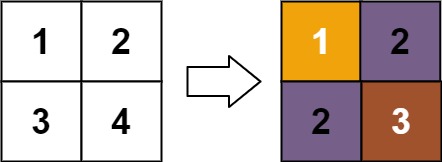
Input: matrix = [[1,2],[3,4]]Output: [[1,2],[2,3]]Explanation:The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.
Example 2:
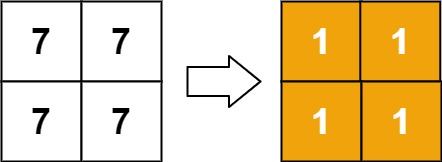
Input: matrix = [[7,7],[7,7]]Output: [[1,1],[1,1]]
Example 3:
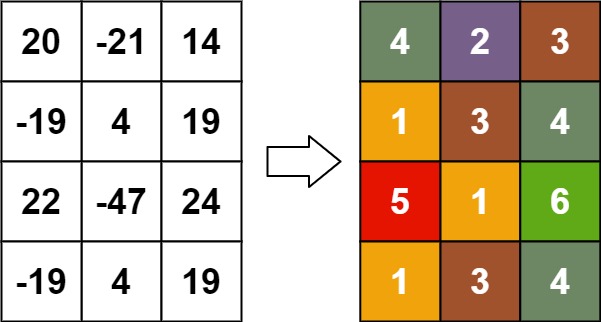
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]
Example 4:
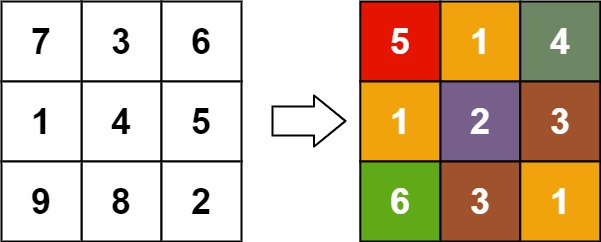
Input: matrix = [[7,3,6],[1,4,5],[9,8,2]]Output: [[5,1,4],[1,2,3],[6,3,1]]
Constraints:
- t
m == matrix.lengthtn == matrix[i].lengtht1 <= m, n <= 500t-109 <= matrix[row][col] <= 109
Sol
數字的自己的行與列的rank都是一樣的
所以需要一個方式記錄目前該行與該列最小的rank,之後取大的 同時,因為前面提到數字的自己的行與列的rank都是一樣的,所以同一行列的最小rank會因為這格被串在一起
說到串,就是同一祖先,說到同一祖先就是union find
class Solution:
def matrixRankTransform(self, mx: List[List[int]]) -> List[List[int]]:
def find(uf,i):
if uf[i] != i:
uf[i] = find(uf,uf[i])
return uf[i]
v2ps = defaultdict(list)
for i in range(len(mx)):
for j in range(len(mx[i])):
v2ps[mx[i][j]].append((i,j))
rank = defaultdict(int)
for v in sorted(v2ps.keys()):
uf = list(range(len(mx)+len(mx[0])))
now = rank.copy()
for (x,y) in v2ps[v]:
x,y = find(uf,x),find(uf,y+len(mx))
uf[x] = y # x -> y, direct to y
now[y] = max(now[x],now[y]) # update rank at y
for (x,y) in v2ps[v]:
rank[x] = rank[y+len(mx)] = mx[x][y] = now[find(uf,x)]+1 # search from x to y+len(mx), then get the cureent smallest rank
return mx