動機
找右邊的最小,之後重建tree
Problem
Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.
Basically, the deletion can be divided into two stages:
- t
- Search for a node to remove. t
- If the node is found, delete the node.
Follow up: Can you solve it with time complexity O(height of tree)?
Example 1:
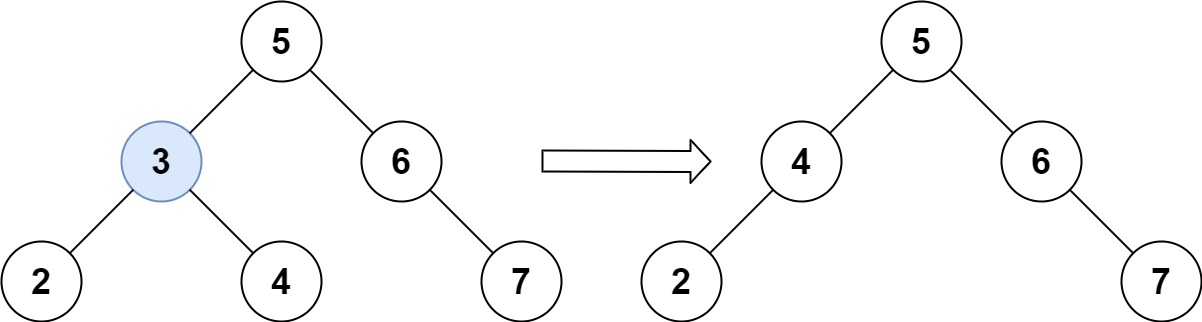
Input: root = [5,3,6,2,4,Leetcode,7], key = 3Output: [5,4,6,2,null,null,7]Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.One valid answer is [5,4,6,2,null,null,7], shown in the above BST.Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.
Example 2:
Input: root = [5,3,6,2,4,null,7], key = 0Output: [5,3,6,2,4,null,7]Explanation: The tree does not contain a node with value = 0.
Example 3:
Input: root = [], key = 0Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -105 <= Node.val <= 105- Each node has a unique value.
rootis a valid binary search tree.-105 <= key <= 105
Sol
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root:
return None
elif root.val > key:
root.left = self.deleteNode(root.left, key)
return root
elif root.val < key:
root.right = self.deleteNode(root.right, key)
return root
else:
if not root.left and not root.right:
return None
elif not root.left:
return root.right
elif not root.right:
return root.left
else:
# find min in root.right
now = root.right
prev = root
while now.left:
prev, now = now, now.left
if now == root.right: # no left
now.left = root.left
else:
prev.left = now.right
now.left = root.left
now.right = root.right
return now