動機
原來這題是greedy阿
Problem
You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
A closed interval [a, b] (with a < b) denotes the set of real numbers x with a <= x <= b.
The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].
Example 1:
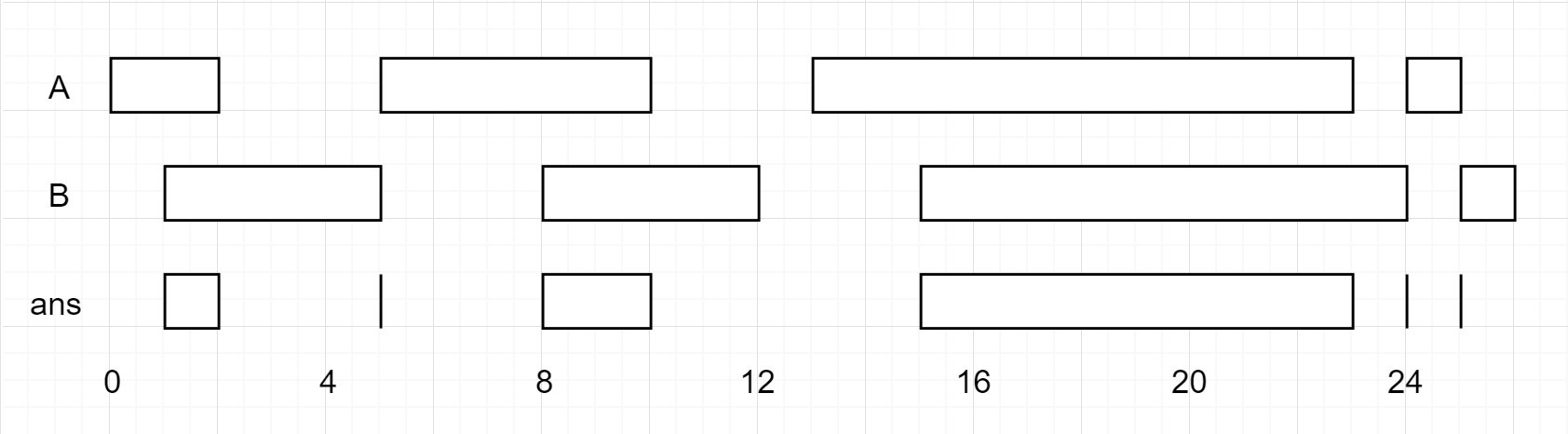
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Example 2:
Input: firstList = [[1,3],[5,9]], secondList = []Output: []
Example 3:
Input: firstList = [], secondList = [[4,8],[10,12]]Output: []
Example 4:
Input: firstList = [[1,7]], secondList = [[3,10]]Output: [[3,7]]
Constraints:
0 <= firstList.length, secondList.length <= 1000firstList.length + secondList.length >= 10 <= starti < endi <= 109endi < starti+10 <= startj < endj <= 109endj < startj+1
Sol
當成interval merge
class Solution:
def intervalIntersection(self, f1: List[List[int]], f2: List[List[int]]) -> List[List[int]]:
if f1 and f2:
if f1[0][0] > f2[0][0]:
return self.intervalIntersection(f2,f1)
elif f1[0][1] < f2[0][1]:
if f1[0][1] < f2[0][0]:
return self.intervalIntersection(f1[1:],f2)
else:
return [[f2[0][0], f1[0][1]]] + self.intervalIntersection(f1[1:],f2)
elif f1[0][1] > f2[0][1]:
return [f2[0]] + self.intervalIntersection(f1,f2[1:])
else: # ==
return [[max(f1[0][0],f2[0][0]), f1[0][1]]] + self.intervalIntersection(f1[1:],f2)
else:
return []
但其實只要看兩個interval的最高最低,在最高最低的值怪怪的就不管
class Solution:
def intervalIntersection(self, firstList: List[List[int]], secondList: List[List[int]]) -> List[List[int]]:
A = firstList
B = secondList
ans = []
i = j = 0
while i < len(A) and j < len(B):
# Let's check if A[i] intersects B[j].
# lo - the startpoint of the intersection
# hi - the endpoint of the intersection
lo = max(A[i][0], B[j][0])
hi = min(A[i][1], B[j][1])
if lo <= hi:
ans.append([lo, hi])
# Remove the interval with the smallest endpoint
if A[i][1] < B[j][1]:
i += 1
else:
j += 1
return ans