動機
lee215的解法依舊漂亮
Problem
In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the ith domino, so that tops[i] and bottoms[i] swap values.
Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.
If it cannot be done, return -1.
Example 1:
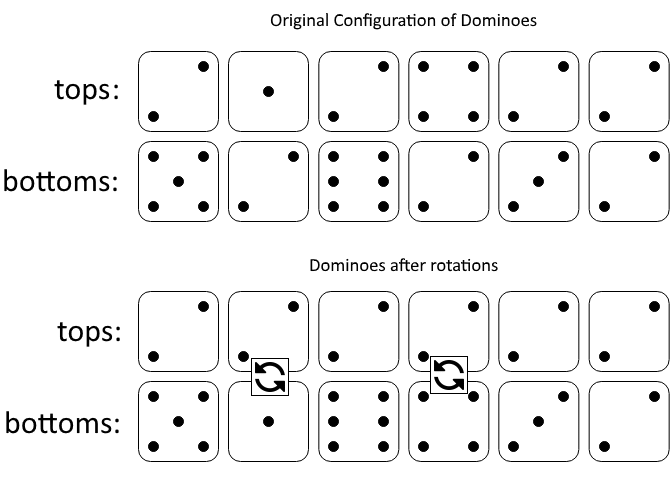
Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]Output: 2Explanation: The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.
Example 2:
Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]Output: -1Explanation: In this case, it is not possible to rotate the dominoes to make one row of values equal.
Constraints:
2 <= tops.length <= 2 * 104bottoms.length == tops.length1 <= tops[i], bottoms[i] <= 6
Sol
就六個數字就是看有沒有就好
class Solution:
def minDominoRotations(self, tops: List[int], bottoms: List[int]) -> int:
for n in range(1,7):
good = True
lhs = rhs = 0
for a,b in zip(tops,bottoms):
if n not in (a,b):
good = False
break
elif n == a and n != b:
lhs += 1
elif n == b and n != a:
rhs += 1
if good:
return min(lhs, rhs)
return -1