動機
post order很重要!!
Problem
Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
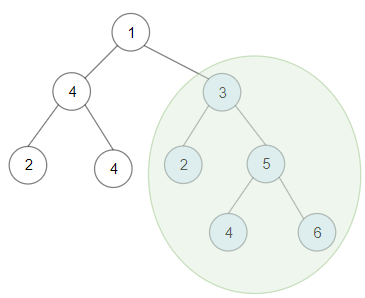
Input: root = [1,4,3,2,4,2,5,Leetcode,null,null,null,null,null,4,6]Output: 20Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.
Example 2:
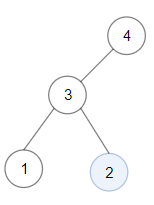
Input: root = [4,3,null,1,2]Output: 2Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.
Example 3:
Input: root = [-4,-2,-5]Output: 0Explanation: All values are negatives. Return an empty BST.
Example 4:
Input: root = [2,1,3]Output: 6
Example 5:
Input: root = [5,4,8,3,null,6,3]Output: 7
Constraints:
- The number of nodes in the tree is in the range
[1, 4 * 104]. -4 * 104 <= Node.val <= 4 * 104
Sol
這裡要處理
- 加總
- 驗證BST
如果從上到下,會很痛苦;所以要想起從底部往上也是tree,可以一步一步往上加與驗證
class Solution:
def maxSumBST(self, root: TreeNode) -> int:
ret = 0
def post(root):
nonlocal ret
if not root:
return [float('inf'), float('-inf'), 0]
else:
lmin, lmax, lsum = post(root.left)
rmin, rmax, rsum = post(root.right)
if lsum is not None and rsum is not None and lmax < root.val < rmin:
ret = max(ret, root.val+lsum+rsum)
return [min(lmin,root.val), max(root.val, rmax), root.val+lsum+rsum]
else:
return [0,0,None]
post(root)
return ret