動機
原來有symmetric difference
Problem
Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).
Return true if all the rectangles together form an exact cover of a rectangular region.
Example 1:
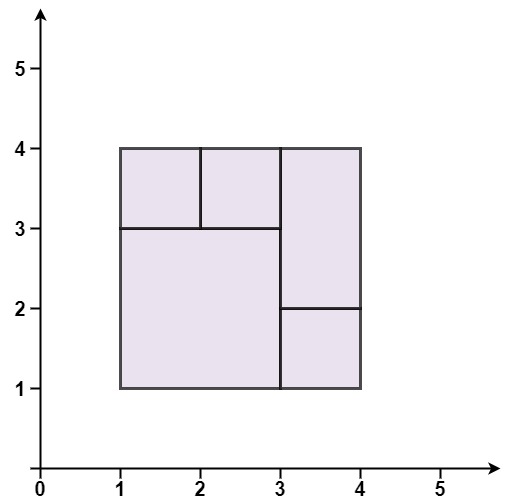
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]Output: trueExplanation: All 5 rectangles together form an exact cover of a rectangular region.
Example 2:
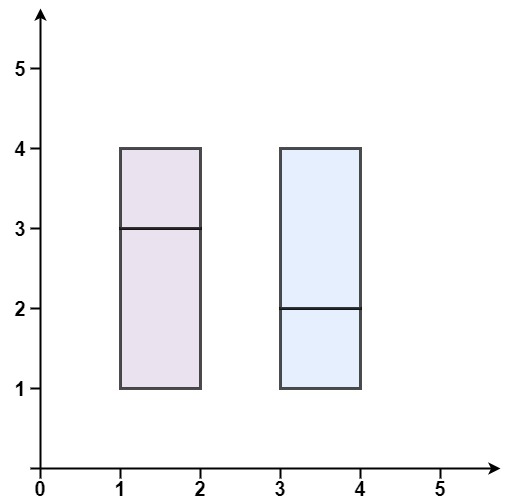
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]Output: falseExplanation: Because there is a gap between the two rectangular regions.
Example 3:
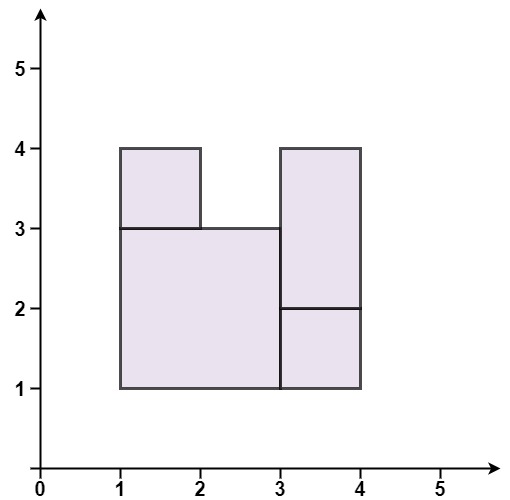
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]Output: falseExplanation: Because there is a gap in the top center.
Example 4:
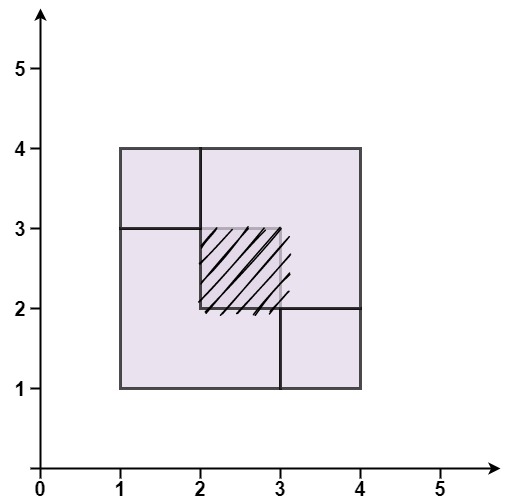
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]Output: falseExplanation: Because two of the rectangles overlap with each other.
Constraints:
1 <= rectangles.length <= 2 * 104rectangles[i].length == 4-105 <= xi, yi, ai, bi <= 105
Sol
symmetric difference: 把同樣的去掉不同的加進來
這樣處理overlay就很簡單,最後看點是不是最大的4個點就好
class Solution:
def isRectangleCover(self, rects: List[List[int]]) -> bool:
points = set()
xl,yl, xh,yh = float('inf'), float('inf'), float('-inf'), float('-inf')
area = 0
for x1,y1,x2,y2 in rects:
xl, yl = min(xl, x1), min(yl, y1)
xh, yh = max(xh, x2), max(yh, y2)
area += (y2-y1)*(x2-x1)
points ^= {(x1,y1), (x1,y2), (x2,y1), (x2,y2)}
#print(points, area, (xl,xh), (yl,yh))
return points == {(xl,yl), (xl, yh), (xh, yl), (xh, yh)} and area == (xh-xl)*(yh-yl)