動機
在你疑惑怎麼在x軸做linesweep時,lee215直接從y軸做離散化!!
Problem
We are given a list of (axis-aligned) rectangles. Each rectangle[i] = [xi1, yi1, xi2, yi2] , where (xi1, yi1) are the coordinates of the bottom-left corner, and (xi2, yi2) are the coordinates of the top-right corner of the ith rectangle.
Find the total area covered by all rectangles in the plane. Since the answer may be too large, return it modulo 109 + 7.
Example 1:
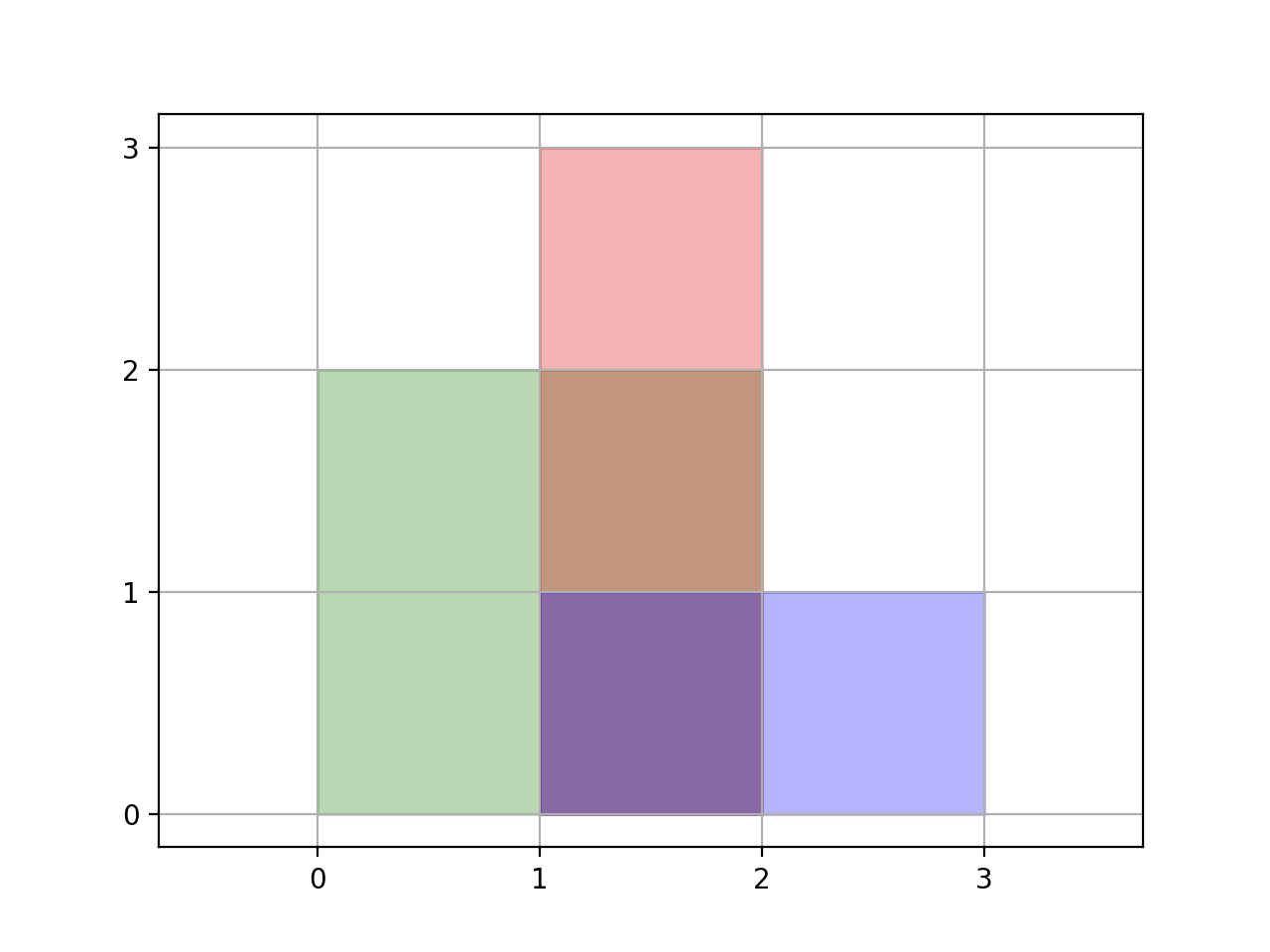
Input: rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]Output: 6Explanation: As illustrated in the picture.
Example 2:
Input: rectangles = [[0,0,1000000000,1000000000]]Output: 49Explanation: The answer is 1018 modulo (109 + 7), which is (109)2 = (-7)2 = 49.
Constraints:
1 <= rectangles.length <= 200rectanges[i].length = 40 <= rectangles[i][j] <= 109- The total area covered by all rectangles will never exceed
263 - 1and thus will fit in a 64-bit signed integer.
Sol
紀錄y軸被覆蓋的區域,加總
class Solution:
def rectangleArea(self, rectangles: List[List[int]]) -> int:
xs = sorted(set([x for x1,y1,x2,y2 in rectangles for x in [x1,x2]]))
x2i = {x:i for i,x in enumerate(xs)}
ystate = [0]*len(x2i)
timeline = sorted([[y,x1,x2,seg] for x1,y1,x2,y2 in rectangles for y,seg in [[y1,1],[y2,-1]]])
cur_y = xsum = area = 0
for y,x1,x2,seg in timeline:
area += (y-cur_y) * xsum
cur_y = y
for i in range(x2i[x1],x2i[x2]):
ystate[i] += seg
xsum = sum(x2-x1 if c else 0 for x1,x2,c in zip(xs,xs[1:],ystate))
return area % (10**9 + 7)