各種平衡樹

動機

補完以前的記憶，下面會介紹

經典款: red-black tree
- 但在面試或是競賽馬上code出來應該有點難，所以通常用下面兩種
rotation base: splay tree
merge/split base: treap

red-black tree

只要符合下面兩個限制的tree就是red-black tree

紅的不會和紅的接在一起

雙紅矛盾

從根到任意leaf的路徑長度都一樣長

黑高矛盾 (不等高)

insert (雙紅矛盾)

insert如何不破壞兩個條件?

黑高矛盾: 每次都插入紅的雙紅矛盾:

插入點是root，child有紅

把root換成黑

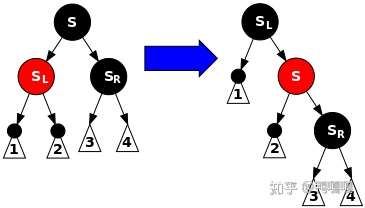
插入點是child (parent是黑的，並假設插在左邊)
左的child是紅的: 直接右旋
右的child是紅的: 左旋再右旋

插右邊的case? 這是對稱的，所以不列了

可以注意到，第2個case的所有case的結果都會是

根是紅的
像這種/\形狀

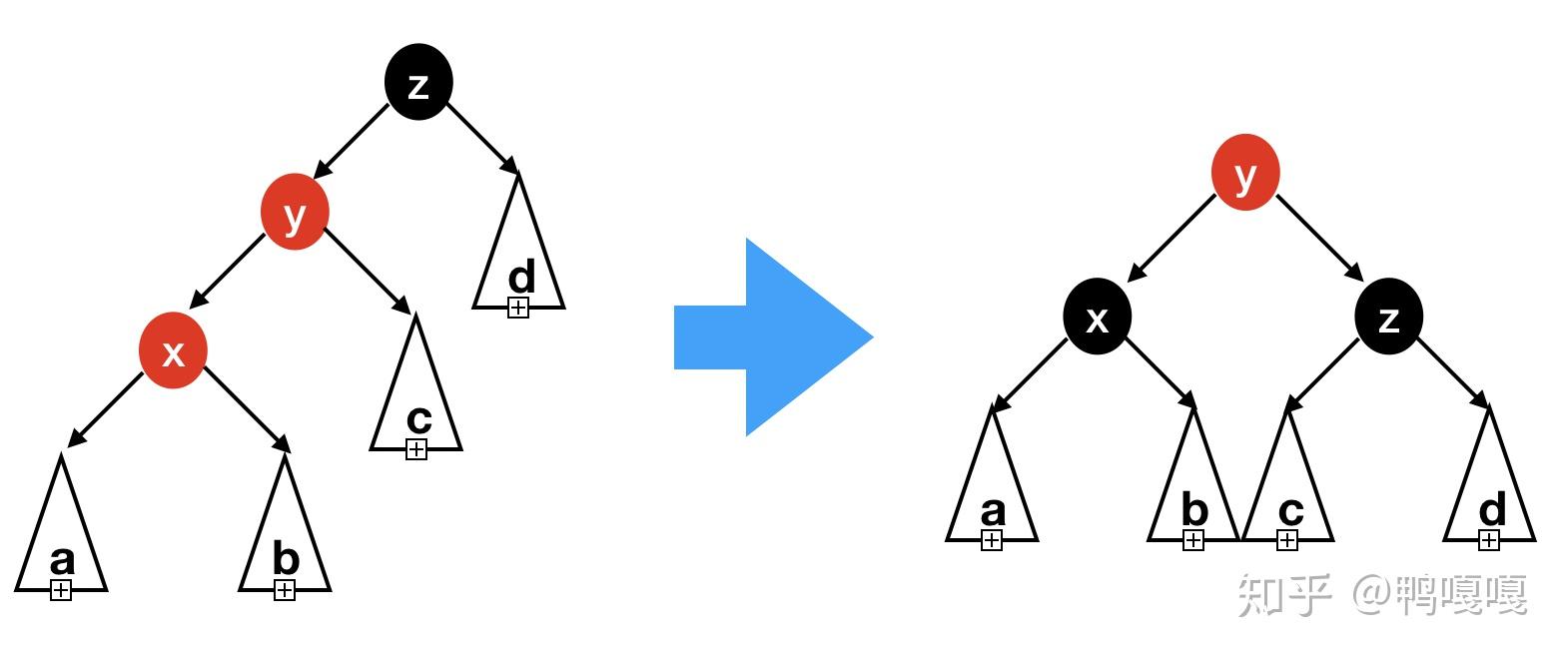
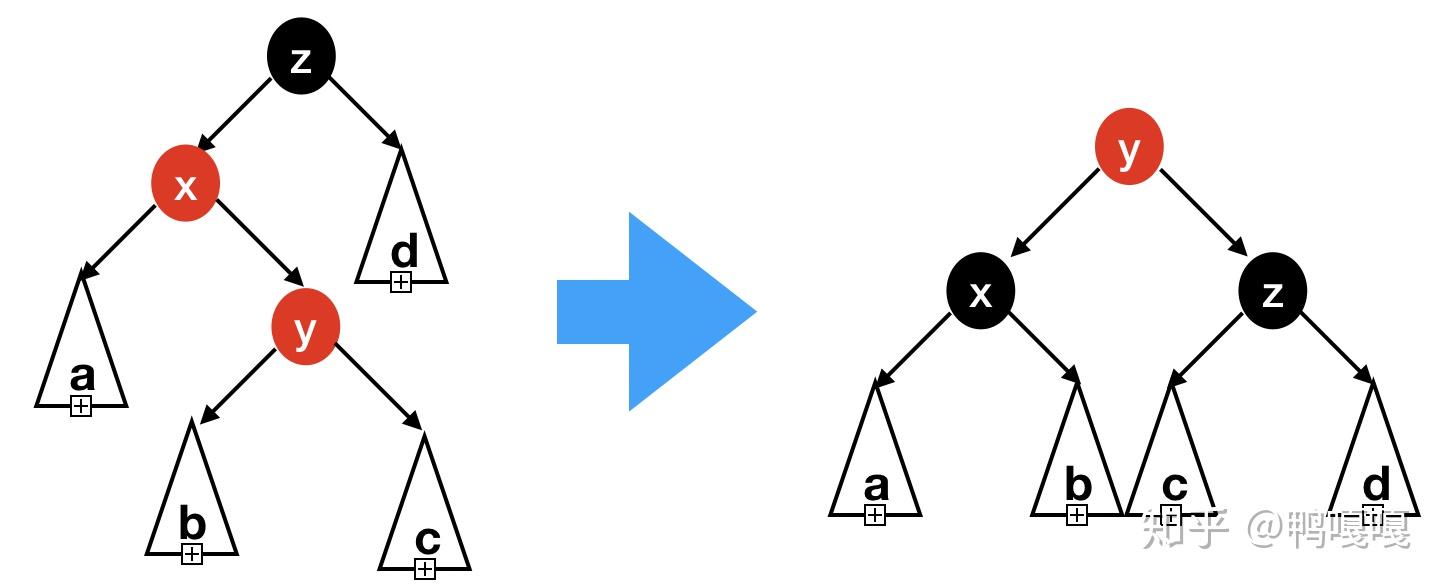
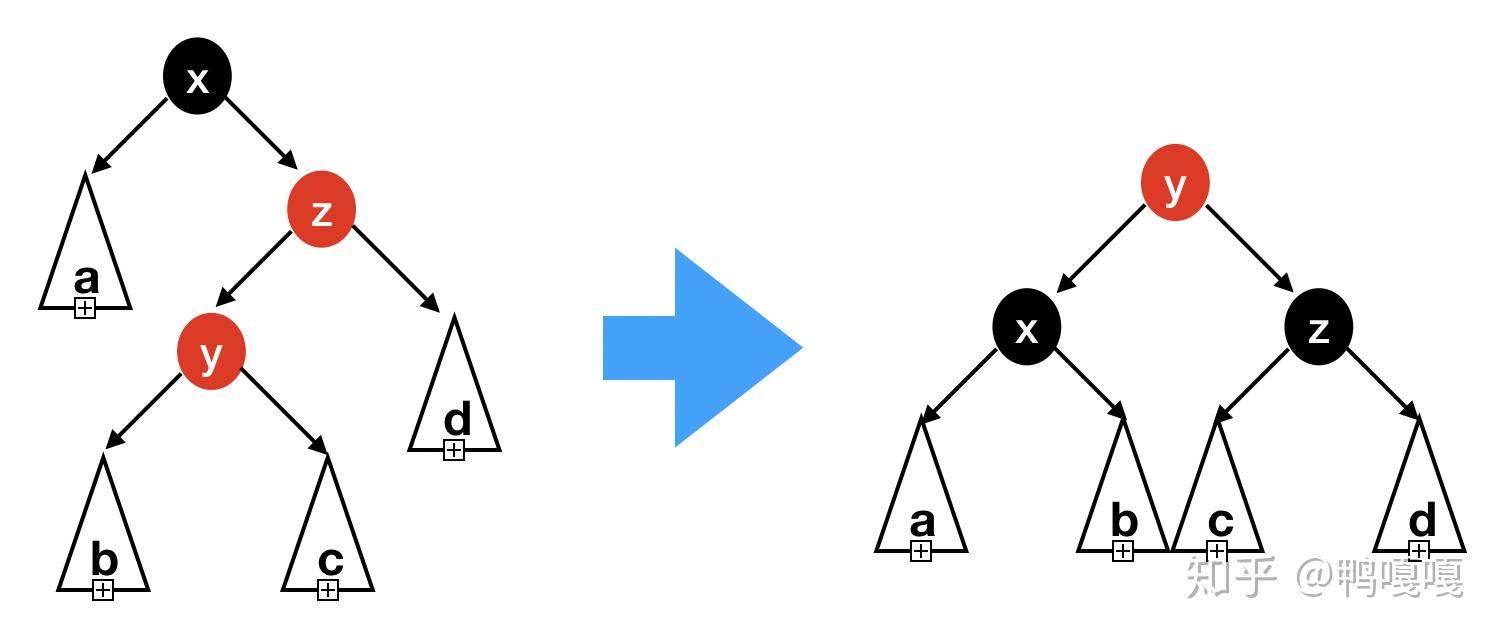
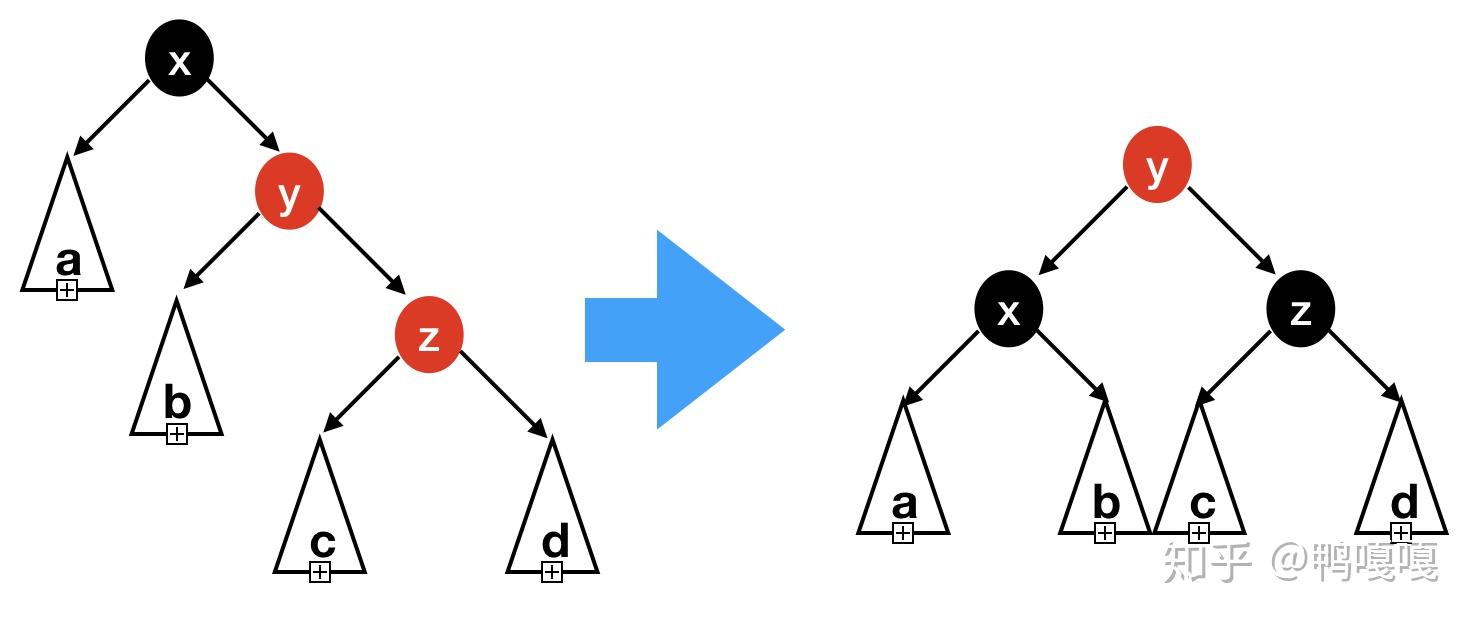
剛剛提到左旋與右旋，來完成再平衡，但是haskell可以直接build資料，所以…

blacken Nil = Nil
blacken (Node _ value left right) = Node Black value left right

insert x root = blacken $ insert' root
  where insert' Nil = Node Red x Nil Nil
        insert' root@(Node color y left right) 
            | x < y = balance color y (insert' left) right
            | x > y = balance color y left (insert' right)
            | otherwise = root

-- left-right
balance Black z (Node Red x a (Node Red y b c)) d = Node Red y (Node Black x a b) (Node Black z c d)
-- left-left
balance Black z (Node Red y (Node Red x a b) c) d = Node Red y (Node Black x a b) (Node Black z c d)
-- right-left
balance Black x a (Node Red y b (Node Red z c d)) = Node Red y (Node Black x a b) (Node Black z c d)
-- right-right
balance Black x a (Node Red z (Node Red y b c) d) = Node Red y (Node Black x a b) (Node Black z c d)
balance color value left right = Node color value left right

delete (黑高矛盾)

delete就是BST的delete

在leaf: 換成nil
只有一個child: 把唯一個child拉上去
兩個child: 右child最小的換上來，再把它刪掉

所以現在重點是換下去的那個點怎麼刪

刪的是

紅的: 沒事
黑的: 數量可能不對 (黑高矛盾)

(把紅的看成收束下面的兩個child成一條長度，因為兩邊的長度一樣) (紅的可以輕易變成黑的，但黑的不行直接變成紅的) 要刪的是黑的，所以可以從parent與neighbor的顏色生出4種case

	root: red	root: black
neighbor: red	impossible	左旋，原本的parent變紅
neighbor: black	原本的parent變黑，neighbor變紅	neighbor變紅

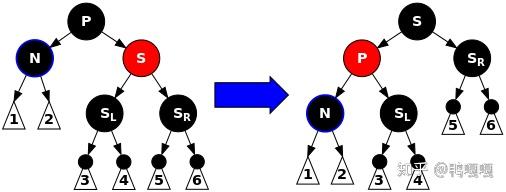
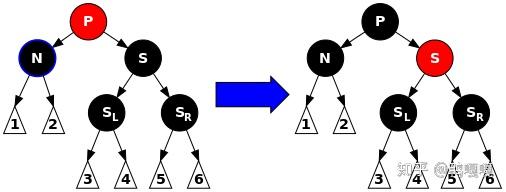
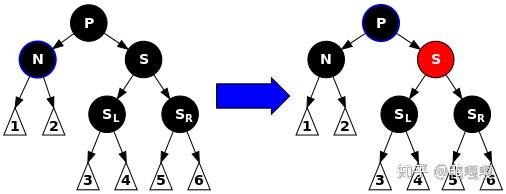
neighbor變紅，不會觸發雙紅矛盾? 有可能，如果兩個child都是黑的就沒事，其中一個是紅的就要處理了

只有右邊是紅、兩個紅: 左旋 (把長度補回去)，把紅的標成黑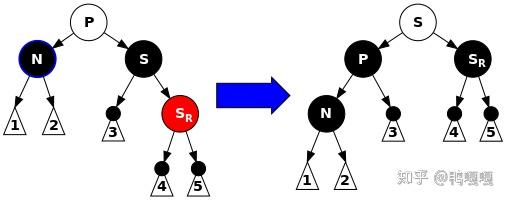只有左邊是紅: 先左旋，轉成一條就可以用前面的方法了

isBlack (Node Red _ _ _) = False
isBlack _ = True

balL color y (left, True) right = (Node color y left right, True)
balL color y (left, False) right = balL' color y left right

balL' color1 p n (Node color2 s sl sr)
    -- neighbor: red, root: black 
    | color2 == Red = balL Black s (balL' Red p n sl) sr
    -- neighbor: black, root: black OR red
    | isBlack sl && isBlack sr = (Node Black p n (Node Red s sl sr), color1 == Red)
    -- 只有右邊是紅、兩個紅
    | not (isBlack sr) = (Node color1 s (Node Black p n sl) (blacken sr), True)
    -- 只有左邊是紅
    | otherwise = let (Node Red x sll slr) = sl in balL' color1 p n (Node Black x sll (Node Red s slr sr))

把剩下的列完

findMin (Node _ x Nil _) = x
findMin (Node _ _ left _) = findMin left

balR color y left (right, True) = (Node color y left right, True)
balR color y left (right, False) = balR' color y left right

balR' color1 p (Node color2 s sl sr) n
    | color2 == Red = balR Black s sl (balR' Red p sr n)
    | isBlack sl && isBlack sr = (Node Black p (Node Red s sl sr) n, color1 == Red)
    | not (isBlack sl) = (Node color1 s (blacken sl) (Node Black p sr n), True)
    | otherwise = let (Node Red x srl srr) = sr in balR' color1 p (Node Black x (Node Red s sl srl) srr) n

delete x t = fst $ delete' x t
  where delete' x Nil = (Nil, True)
        delete' x root@(Node color y left right)
            | x < y = balL color y (delete' x left) right
            | x > y = balR color y left (delete' x right)
            | otherwise = deleteRoot root
        deleteRoot (Node color _ Nil Nil) = (Nil, color == Red)
        deleteRoot (Node _ _ left Nil) = (blacken left, True)
        deleteRoot (Node _ _ Nil right) = (blacken right, True)
        deleteRoot (Node color _ left right) = let m = findMin right in balR color m left (delete' m right)

Ref 有人能讲清楚《Algorithms》中左倾红黑树（LLRB）删除操作的每一行代码吗？

splay tree

利用特別的旋轉(splay)，把最近存取的點轉到root，達成所有操作均攤log n

如果只有父節點，也就是父節點是root，就直接rotate 但如果有祖父節點時要做下面兩個case的旋轉

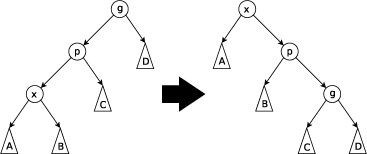
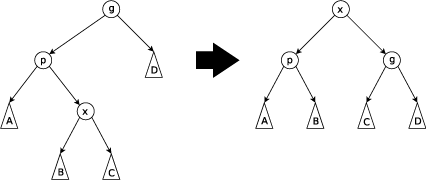
Q: 為什麼這個rotate這麼特別，如果說只是轉上去，其實不用管祖父節點? A: 這樣才能確保出來的深度是最小的

P.S.: C++的rotate很複雜，因為一次只能assign一次，所以狀態一直變，但是利用平行賦值就好很多

每次改node，都要確認被改過的node的left, right, parent都是對的!!

class Node:
  def __init__(self, key:int = 0, parent = None, left = None, right = None):
    self.key, self.parent, self.left, self.right = key, paretn, left, right

  def left_rotate(self):
    oldroot, newroot = self, self.left

    newroot.parent, oldroot.parent = oldroot.parent, newroot
    newroot.right, oldroot.left = oldroot, newroot.right

    if newroot.left:
      newroot.left.parent = oldroot
    if newroot.parent:
      if newroot.parent.left is oldroot:
        newroot.parent.left = newroot
      else:
        newroot.parent.right = newroot

  def right_rotate(self):
    oldroot, newroot = self, self.right

    newroot.parent, oldroot.parent = oldroot.parent, newroot
    newroot.left, oldroot.right = oldroot, newroot.right

    if newroot.right:
      newroot.right.parent = oldroot
    if newroot.parent:
      if newroot.parent.left is oldroot:
        newroot.parent.left = newroot
      else:
        newroot.parent.right = newroot
  
  def is_left(self, other):
    return self.left is other

  def splay(self):
    while self.parent:
      parent, grand_parent = self.parent, self.parent.parent
      if grand_parent:
        if grand_parent.is_left(self.parent):
          if left_child:
            grand_parent.left_rotation()
            parent.left_rotation()
          else:
            parent.right_rotation()
            grand_parent.left_rotation()
        else:
          if not left_child: # is right child
            grand_parent.right_rotation()
            parent.right_rotation()
          else:
            parent.left_rotation()
            grand_parent.right_rotation()
      else:
        # zig
        if parent.left is self:
          parent.left_rotate()
        else:
          parent.right_rotate()
  
  def find(self, key: int) -> Node:
    ret = None
    if self.key == key:
      ret = self
    elif self.right and self.key < key:
      ret = self.right.find(key)
    elif self.left and self.key > key:
      ret = self.left.find(key)
    return ret

  def find_min(self):
    return self.left.find_min() if self.left else self.key

insert與BST差不多，但是最後要splay!!

def insert(root: Node, key: int):
  ## WTF
  prev: Node, now: Node = None, root

  while now:
      prev, now = now, now.right if now.key < key else now.left
  
  now = Node(key, prev)
  if prev.key < now.key:
      prev.right = now
  else:
      prev.left = now
  
  now.splay()

基本就是BST的remove，但要先把target splay，再做BST的remove

def remove(root, key):
    ## WTF
    target: Node = root.find(key)

    def take_place(a, b):
        if b:
          b.parent = a.parent
        if a.parent:
          if a.parent.left is a:
            a.parent.left = b
          else:
            a.parent.right = b

    if target:
        target.splay()

        if not target.left:
            take_place(target, target.right)
        elif not target.right:
            take_place(target, target.left)
        else:
            miniumum = target.right.find_min()

            if miniumum.parent is not target:
                take_place(miniumum, miniumum.right)
                miniumum.right = target.right
                miniumum.right.parent = miniumum
            take_place(target, miniumum)
            miniumum.left = target.left
        del target

Ref

treap

每個點都有

key: BST的val
pri: heap的比較數字所以叫tree + heap = treap

在維持heap的前提下(意思是heap先滿足)，滿足BST的需求

同時treap有以下性質

給定 n 個節點的 key、pri 的大小關係，那麼這棵 treap 的形狀唯一。
給定 n 個節點的 key，在 n 個節點的 pri 都隨機的前提下（也就是 treap 的形狀隨機），任一個選定的節點的期望深度為 O(log n)。

所以根據第2點，我們pri要是random

class Node:
  def __init__(self, key: int = 0, left = None, right = None):
    self.left, self.right = left, right
    self.key, self.pri = key, random()
  
  def inspect(self) -> [int]:
    ret = [self.key]
    ret += self.left.inspect() if self.left else []
    ret += self.right.inspect() if self.right else []
    return ret
  
  def size(self) -> int:
    ret = 1
    ret += self.left.size() if self.left else 0
    ret += self.right.size() if self.right else 0
    return ret

有rotate的寫法，但很複雜，同時有merge/split的寫法，好寫很多，所以做merge/split

split: 把一顆樹根据數字分成左右兩顆treap

root key比較小就跟左邊、比較大就跟右邊，剩下的(另一側)拿去遞迴，繼續割 merge: 依據pri與key合併兩棵treap
同時限制左邊的treap的所有key都小於右邊的treap
- 只要是合併split後的treap就可以滿足這個限制
- merge/split互為反函數

def split(root: Node, key: int) -> [Node, Node]:
  if not root:
    return [None, None]
  elif root.key <= key:
    # 保留 root.left
    # 繼續分 root.right，之後接上新的treap
    l, r = split(root.right, key)
    root.right = l
    return [root, r]
  else:
    l, r = split(root.left, key)
    root.left = r
    return [l, root]

def merge(l: Node, r: Node) -> Node:
  if not l or not r:
    return l or r
  elif l.pri > r.pri:
    l.right = merge(l.right, r)
    return l # 讓pri大的當root
  else:
    r.left = merge(l, r.left)
    return r # 讓pri大的當root

insert:

基本上就是BST insert，但是還有pri!!
所以可以先看pri，如果比較大就插這裡 (用split生左右tree!!)

def insert(root: Node, target: Node):
  if not root:
    return target
  elif target.pri > root.pri:
    target.left, target.right = split(root, target.key)
    return target
  else:
    # usual BST insert
    if root.key <= target.key:
      return insert(root.right, target)
    else:
      return insert(root.left, target)

remove:

遠比BST的remove簡單!!
遇到要刪的，直接merge原有的左右tree!!

def remove(root: Node, key: int) -> Node:
  if not root:
    return None
  elif root.key == key:
    return merge(root.left, root.right)
  else:
    if root.key <= key:
       root.right = remove(root.right, key)
    else:
      root.left = remove(root.left, key)
    return root

這個是set的union，作法就是用最大pri的treap作主軸，一直split右邊的treap，之後就是繼續unite被split出來的treap

def unite(l: Node, r: Node) -> Node:
  if not l or not r:
    return l or r
  elif l.pri < r.pri:
    return unite(r, l)
  else:
    r_left, r_right = split(r, l.key)
    l.left = unite(l.left, r_left)
    l.right = unite(l.right, r_right)
    return l

Ref

動機#

red-black tree#

insert (雙紅矛盾)#

delete (黑高矛盾)#

splay tree#

treap#

動機

red-black tree

insert (雙紅矛盾)

delete (黑高矛盾)

splay tree

treap