動機
複習tarjan dfs,要在40分鐘內想出來是可能的嗎? 另外,第一次遇到無向圖,在奇怪的的地方卡很久…
Problem
There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [ai, bi] represents a connection between servers ai and bi. Any server can reach other servers directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some servers unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
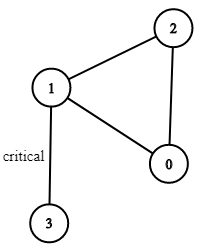
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]Output: [[1,3]]Explanation: [[3,1]] is also accepted.
Example 2:
Input: n = 2, connections = [[0,1]]Output: [[0,1]]
Constraints:
2 <= n <= 105n - 1 <= connections.length <= 1050 <= ai, bi <= n - 1ai != bi- There are no repeated connections.
sol
class Solution:
def setTime(self,node):
self.ts += 1
self.early[node] = self.time[node]= self.ts
self.visited.add(node)
def dfs(self, node, root):
self.setTime(node)
for child in self.graph[node]:
if root != child:
if child in self.visited:
self.early[node] = min(self.early[node], self.time[child])
else:
# tree edge
self.dfs(child, node)
self.early[node] = min(self.early[node], self.early[child])
if self.early[child] > self.time[node]:
self.bri.append([node, child])
def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:
self.bri = []
self.early = {}
self.time = {}
self.ts = 0
self.graph = defaultdict(list)
self.visited = set()
[self.graph[k].append(v) for (k,v) in connections]
[self.graph[v].append(k) for (k,v) in connections]
[self.dfs(i, i) for i in range(n) if i not in self.visited]
#print(f'{self.early} {self.time}')
return self.bri