動機
oh Floyd-Warshall,我忘了!! 原來還可以這樣解loop
Problem
There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the second lane and wants to jump to point n. However, there could be obstacles along the way.
You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at point i. If obstacles[i] == 0, there are no obstacles at point i. There will be at most one obstacle in the 3 lanes at each point.
- For example, if
obstacles[2] == 1, then there is an obstacle on lane 1 at point 2.
The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle on the new lane.
- For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.
Return the minimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.
Note: There will be no obstacles on points 0 and n.
Example 1:
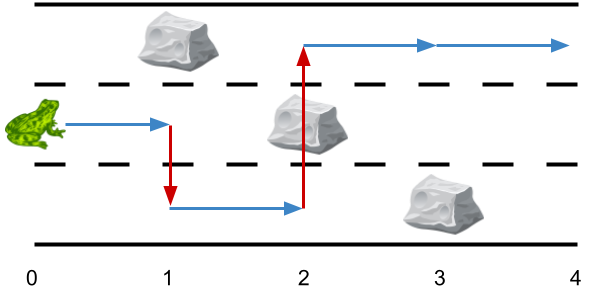
Input: obstacles = [0,1,2,3,0]Output: 2 Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).
Example 2:
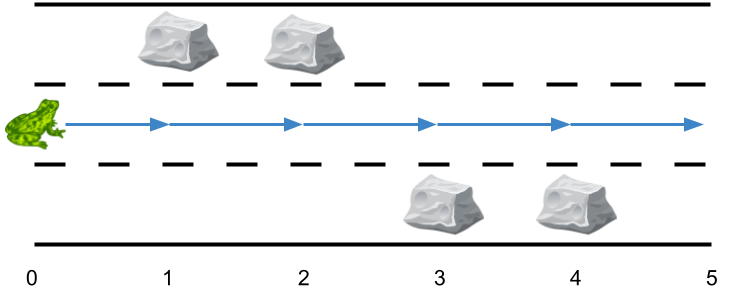
Input: obstacles = [0,1,1,3,3,0]Output: 0Explanation: There are no obstacles on lane 2. No side jumps are required.
Example 3:
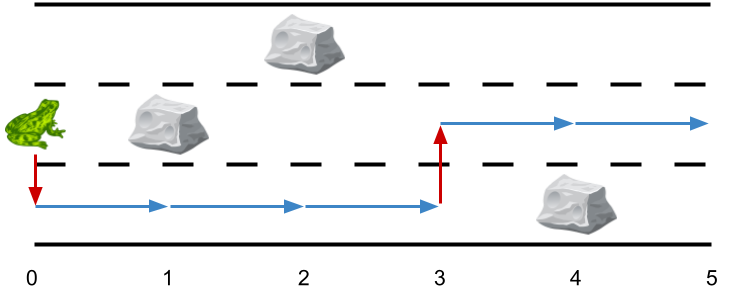
Input: obstacles = [0,2,1,0,3,0]Output: 2Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps.
Constraints:
obstacles.length == n + 11 <= n <= 5 * 1050 <= obstacles[i] <= 3obstacles[0] == obstacles[n] == 0
sol
原本想用熟悉的方法解dp,之後就遇到很尷尬的狀態,對於不同障礙的分佈組合會處理到死
但這是path,我們有relax!! 所以可以一直relax!!
class Solution:
def minSideJumps(self, obstacles: List[int]) -> int:
dp = [float("inf"), 0, float("inf")]
for o in obstacles:
o -= 1
if o != -1:
dp[o] = float("inf")
for l in range(3):
if l != o:
dp[l] = min(dp[l], dp[(l+1) % 2]+1, dp[(l+2) % 3]+1)
# walk multiple times!!
print(f'{dp}')
return min(dp)