動機
leetcode復健,原本以為只是複習topo sort…
Problem
There is a directed graph of n colored nodes and m edges. The nodes are numbered from 0 to n - 1.
You are given a string colors where colors[i] is a lowercase English letter representing the color of the ith node in this graph (0-indexed). You are also given a 2D array edges where edges[j] = [aj, bj] indicates that there is a directed edge from node aj to node bj.
A valid path in the graph is a sequence of nodes x1 -> x2 -> x3 -> ... -> xk such that there is a directed edge from xi to xi+1 for every 1 <= i < k. The color value of the path is the number of nodes that are colored the most frequently occurring color along that path.
Return the largest color value of any valid path in the given graph, or -1 if the graph contains a cycle.
Example 1:
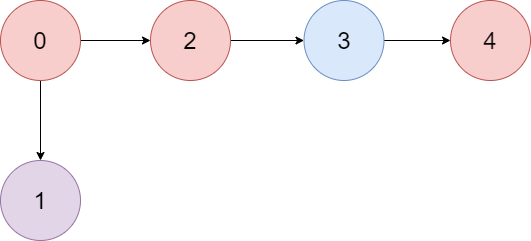
Input: colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]Output: 3Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored "a" (red in the above image).Example 2:
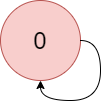
Input: colors = "a", edges = [[0,0]]Output: -1Explanation: There is a cycle from 0 to 0.
Constraints:
n == colors.lengthm == edges.length1 <= n <= 1050 <= m <= 105colorsconsists of lowercase English letters.0 <= aj, bj < n
ver1 TLE: 純topo
我們很懶,所以所有dfs需要的東西都往args裡面丟。
如果是用一個大表表示有沒有被visited過需要多一個狀態是還在dfs中,但這裡是直接放到args裡面所以不用
class Solution:
def dfs(self, graph, node, visited, colors):
colors[self.color[node]] += 1
if node in visited or self.maxCnt == -1:
#print(f'LOOP {node} {visited} {colors}')
self.maxCnt = -1
elif not graph[node]:
#print(f'GOAL {node} {visited} {colors} {colors.most_common(1)}')
self.maxCnt = max(colors.most_common(1)[0][1], self.maxCnt)
else:
visited.add(node)
#print(f'PATH {node} {visited} {colors}')
[self.dfs(graph, k, visited, colors) for k in graph[node] if self.maxCnt != -1]
visited.remove(node)
colors[self.color[node]] -= 1
def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:
self.maxCnt = 0
self.color = ''
G = defaultdict(list)
self.color = colors
[G[k].append(v) for (k,v) in edges]
# 1. list all nodes whose in-degree is 0
degree0 = set(range(len(colors))) - set(v for (k,v) in edges)
#print(f'GGG {degree0} {G}')
[self.dfs(G, k, set(), Counter()) for k in degree0 if self.maxCnt != -1]
return self.maxCnt if degree0 else -1
sol
真的太久沒做LC了,沒想到這是最佳化問題,所以一定是窮舉,有可能是DP或是greedy。 但那這個結構有可以優化的地方嗎? 這是path,而path一定是建構在另一個path上!! 所以可以DP
但該走的還是得走,所以還是topo sort
DP什麼? 我們需要的是某條path最多的(max)顏色數,所有有兩個參數顏色與節點,但節點是哪個節點? 是path的開始還是path的終點?
如果是我會看我想怎麼寫dp如果是top-down(可以直接用@cache)就要是path的開始,如果是bottom-up就要是path的終點。 而是要寫top-down還是bottom-up是看人,大部分兩個都會通,但根據資料的特性有得時候用另一個會有自然的好處,像是如果dp參數有長度就最好從bottom-up。 如果長度未知,像這題,就可以直接top-down,因為top-down會自動分解要處理的對象,而長度就不能這樣做。
不過這個code的效率是超差的,但我只是來復健(python都要一直反覆查api才知道怎麼用…),所以算了,而且code很短,可以容納在白板中
class Solution:
@cache
def dp(self, node, color):
if node in self.visited:
return float("inf")
ans = 1 if self.color[node] == color else 0
if self.graph[node]:
self.visited.add(node)
ans += max(self.dp(k, color) for k in self.graph[node])
self.visited.remove(node)
return ans
def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:
self.colorSet = set(colors)
self.graph = defaultdict(list)
self.color = colors
self.visited = set()
[self.graph[k].append(v) for (k,v) in edges]
ans = max(self.dp(k, c) for k in range(len(colors)) for c in self.colorSet)
#[print(f'{k},{c} :: {self.dp(k,c)}') for k in range(len(colors)) for c in self.colorSet]
return -1 if ans == float("inf") else ans